Quick summary of CART
as found in the paper.
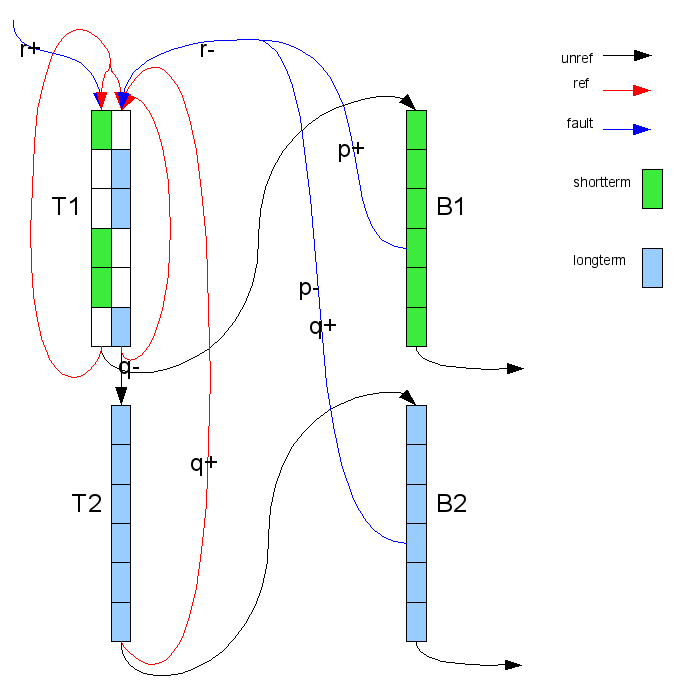
There are four lists: T1, T2, B1 and B2 and two list targets: p and q. The T lists hold resident pages and the B lists hold non-resident pages. The targets are the target sizes of T1 and B2 respectivly. Each page has two bits: the referenced bit and a filter bit. The filter bit distinguishes shortterm vs. longterm usage.
T1 contains both short- and longterm pages and T2 only contains longterm pages. B1 contains shortterm non-resident pages; B2 contains longterm non-resident pages.
On fault a page is checked agains B1 and B2, if present the page becomes a longterm page, otherwise a shortterm page is inserted in T1.
When the need arises to free a page we rotate T2 until it points to an unreferenced longterm page; referenced pages are moved to T1. Then we rotate T1 until it points to an unreferenced shortterm page; longterm pages are moved to T2's head, referenced shortterm pages are moved to T1's head and optinally promoted to longterm pages when T1 exceeds its target size. Then depening on T1's target size p either the T1 or the T2 tail page is reclaimed and placed on B1 or B2 resp. possibly replacing another B page which is determined by B1's size in relation to is target q.
The T1 target size p is a reflection of the number of hits in B1 vs. hits in B2; ie. its incremented on a B1 hit and decremented on a B2 hit.
The T2 target size q is a little more complicated, q almost measures the flux of pages from T2 to T1.
My intuition for the parameter 'q' is as follows. This parameter is the target size for the list B1. It is also varied throughtout the algorithm depending upon movement of pages from T1 -> T2 or T2 -> T1. On a move from T1 -> T2, q is decreased. On a move from T2 -> T1, q is increased. As you point out the trick part is the increment of q. Understanding a croner case will help a lot here. Let us assume that all T2 pages move to T1. At this point the desired size of q is exactly c. Similarly, if T1 is empty and T2 is full, then we would like to keep q again to size c. Observe that it is hits in B1 that generate new T2 pages. --- Dharmendra S Modha
CART Illustrated
p+ |
p = min(p + max(1, ns/|B1|), c) |
p- |
p = max(p - max(1, nl/|B2|), 0) |
q+ |
if (|B2| + nl >= c) q = min(q + 1, 2c - |T1|) |
q- |
q = max(q - 1, c - |T1|) |
r+ |
r = min(r + max(1, ns/nl), c) |
r- |
r = max(r - max(1, nl/ns), 0) |
Adaption to Linux
- Multiple zones
In order to adapt CART to multiple zones I took advantage of the fact that the resident and non-resident lists are nicely seperated. I keep global B lists with target q and per zone T lists with target p. When B/q values are used in T/p context they are scaled.
- Insert Referenced
In order to avoid that new pages are promoted to longterm on their first check PG_new is introduced, it is set when a page enters the T lists and testcleared on T1 rotation. The short- to longterm promotion is skipped when new. (More on PG_new in the CART+ section).
- Expensive Referenced Check
Batching up the reclaim part of CART took a little thought. What I ended up with is this: instead of looking for a single match to the T1 and T2 rotation condition I'd rotate a fixed quanta of pages and isolate those that match the condition; moving the rest off to their resp. places. Then from these two candidate lists I'd p-balance-pick the proper one until I had the required number of reclaimable pages or one or both of the candidate lists dried up, in which case I'd just batch-rotate them again.
- Asynchronous Page-Out
In order to avoid the infinite loop over PG_writeback pages I treat PG_writeback pages as if they were referenced (in order to rotate them as far away as possible) and break the batch-rotate when then number of encountered PG_writeback pages outnumbered the number of candidates.
CART+
CARTs weakness is it's inability to handle cyclic access patterns. I have made an attempt to solve this deficiency. This is done by adding another adaptive parameter: r, which will measure the influx of fresh pages. A fresh page is one that is not on either B1 or B2; ie. r is incremented when the faulted page is not in B otherwise it is decremented.
The reclaim path is then modified to prefer new (PG_new) longterm pages when r drops below the number of longterm pages on the T lists. The idea here is that we want to recognize the situation where we have a saturation of longterm pages and low influx of fresh pages.
This complicates the reclaim path a bit since we now have a possible third candidate list.
A possible improvement to this scheme would be to give these new longterm pages a second chance when T1 falls short of its target; the exact condition for promoting short- to longterm pages; and only reclaim these longterm pages when they are unreferenced on the second cycle.
Nonresident Pages
For keeping track of the onresident pages a datastructure is needed that provides fast lookup and relative order. So far we viewed the nonresident tracking as two lists: B1 and B2; however as we all know lists are not known for their lookup speeds. Hence we need an alternate form. Rik provided a datastructure that almost fit my needs however it only provided for a single list NonResidentPages. I took that idea and modified it to suit my needs.
The general idea is to make a lot of small lists; small enough to search fast but big enough to preserve enough order to be usefull. Use these lists as hash-table buckets and assume that the hash-function has an equal spread.
Since the two lists we need to balance have a total maximum:
|B1| + |B2| <= c
it is possible to break this into smaller lists. Say we take J buckets so that each bucket will have room for c/J entries we can then write for each j of J:
|B1j| + |B2j| <= c/J.
Under the assumption of equal spread we can then write that:
|B1j| / |B2j| = |B1| / |B2|
This leads to the possibility of having small buckets with two lists in them. So instead of the CLOCK per bucket in Rik's code I put in 4. That means not being able to play the atomic game and hence I'm stuck with a spinlock_t in there as well. Each CLOCK is implemented by a circular single linked list of entries. Each entry sacrifices 8 bits in a 2/6 split in order to accomodate this. 2 bits for a list identifier and 6 for the next slot position. (If you wonder why 4 and not 2; it fit. These extra two list heads came for free due to alignment issues and the extra lists actually come in handy. One of them is used as a free list.)
Also because CART makes balance decisions based on the size of the B lists I keep global per-cpu counters for each list. And I remove non-resident entires in the unmap path. In order to achieve that I had to modify the swap-cache to also free possible non-resident entries and added a similar construct to the generic file-cache. This stabilized the behaviour of the algorithm.
Code
The code can be found here.
